Joint work with Yonathan Efroni (equal contribution) and Shie Mannor.
Published at the Thirty-sixth International Conference on Machine Learning (ICML) 2019.
What?
We introduce a new measure of robustness - robustness to action uncertainty. We show that, compared to previous approaches, 'Action Robust Reinforcement Learning' has an efficient solution with convergence guarantees (in the tabular case).
Why?
The recent surge in reinforcement learning research has enabled the field to tackle complex continuous control tasks (i.e., robotics). While these results are impressive, these works share a common pitfall - they, as do all other RL algorithms, overfit to the training set. In practice, the algorithm will not run on exactly the same robot, with exactly the same environmental properties. For instance, a robot might differ in weight, the friction of the joints, the strength of the motors; and the environment may differ in temperature, humidity and more. As the basic RL algorithms are not designed to cope with such conditions, these inconsistencies between the training and testing regimes hinder the ability of current algorithms to tackle real life robotics problems.
While the Robust MDP [1, 2] framework exists, due to it's generality, the results algorithms are inefficient and impractical in real life applications.
How?
We propose the Action Robust approach which, instead of considering robustness with respect to uncertainty in the transition kernel, considers robustness in the performed action. In layman terms, it considers the scenario in which the agent attempts to perform a certain action, but instead a different one is performed.
We consider two forms of uncertainty, the Noisy Robust (NR) and Probabilistic Robust (PR). The former considers the case in which the performed action is a perturbation of the action a we wanted to perform, i.e., (1- α) a + α b, and the latter considers the case in which with probability α instead of the action a being played, the action b is.
We analyze both approaches and show that for the PR strong duality holds (min-max equals max-min). We derive a gradient-based algorithm (Algorithm 2) which is ensured to converge to the Nash equilibrium (in the tabular case).
This algorithm follows 2 simple steps. (i) The optimal policy is found, for a fixed adversary policy, (ii) the adversary is updated towards the 1-step greedy (not the optimal policy, but only a single policy iteration step) worst case policy.
Experiments
Based on Algorithm 2, we derive a robust deep RL approach, based on DDPG [3]. Our approach is composed of 3 networks, an (i) actor, (ii) adversary and (iii) critic. The actor (adversary), similar to DDPG, is trained to maximize (minimize) the action-value function, by taking the gradient through the critic. On the other hand, the critic is trained to evaluate the joint policy.
We compare our approach, AR-DDPG, to DDPG which is trained without an adversary. Additional implementation details, including an ablation test, can be found in our paper. The results below compare the ability of the various approaches to cope with uncertainty. The agents are trained with a relative mass of 1 and a noise probability of 0. During test time, we change the mass of the robot and increase the probability of a random action happening (noise probability).
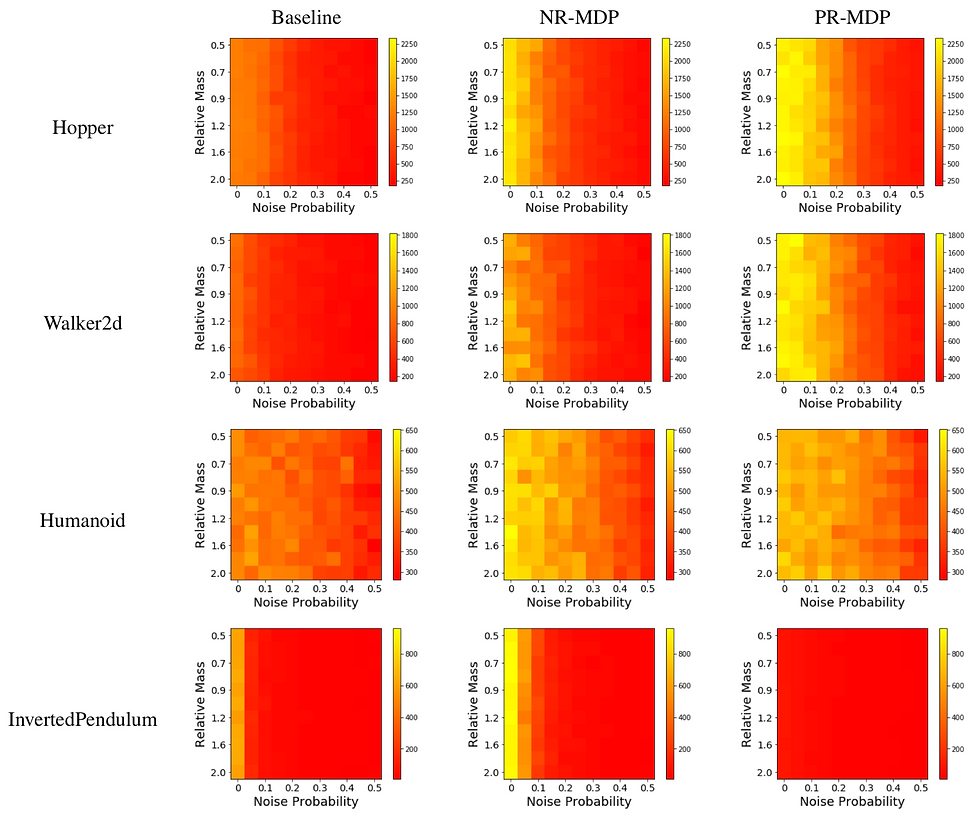
Our approach, Noisy (NR) and Probabilistic (PR) result in policies which are more robust to uncertainty, when compared to the non-robust variant (DDPG). In addition, we notice a surprising result - the performance without adversarial perturbation (i.e., noise probability 0 and relative mass 1) is also improved. We believe that this points towards the adversary acting as a regularizer, forcing the agent to find safer policies, which in turn lead to a better outcome.
Conclusions
We have presented two new criteria for robustness, the Probabilistic and Noisy Action Robust MDP. These criteria are correlated to uncertainty encountered in real-life robotics domains, through which we are able to derive efficient solutions with theoretical guarantees (Algorithm 2).
Based on these theoretical results, we derived a deep reinforcement learning variant and empirically tested its ability to learn robust policies. We notice that our approach not only results in a more robust policy, but the performance without any adversarial intervention is also improved.
Lastly, for solving an action-robust policy, there is no need in providing an uncertainty set. The approach requires only a scalar value, namely α (or possibly a state-dependent α(s)), which implicitly defines an uncertainty set. This is a major advantage compared to standard robust approaches in RL and control, which, to the best of our knowledge, require a distribution over models or perturbations. Of course, this benefit is also a restriction - the Action Robust approach is unable to handle any kind of worst-case perturbations. Yet, due to its simplicity, and its demonstrated performance, it is worthwhile to be considered by an algorithm designer.
Bibliography
[1] Nilim, A. and El Ghaoui, L. Robust control of markov decision processes with uncertain transition matrices. Operations Research, 53(5):780–798, 2005.
[2] Wiesemann, W., Kuhn, D., and Rustem, B. Robust markov decision processes. Mathematics of Operations Research, 38(1):153–183, 2013.
[3] Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T., Tassa, Y., Silver, D., and Wierstra, D. Continuous control with deep reinforcement learning. arXiv preprint arXiv:1509.02971, 2015.
Comments