Stabilizing Off-Policy Reinforcement Learning with Conservative Policy Gradients
- Chen Tessler

- Oct 3, 2019
- 3 min read
Joint work with Nadav Merlis and Shie Mannor.
Under review at the Eighth International Conference on Learning Representations (ICLR) 2020.
What?
In this work, we propose the conservative policy gradient approach, which leverages the similarities between the classic approaches (Policy Iteration) and the more recent deep-learning based (DDPG) in order to improve stability and convergence in practical applications.
Why?
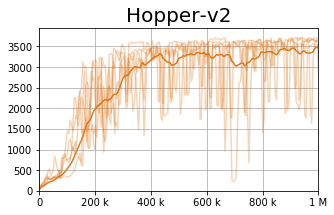
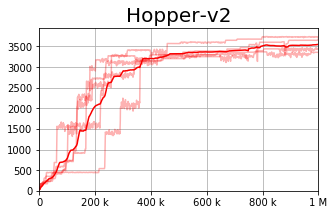
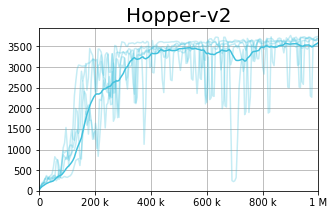
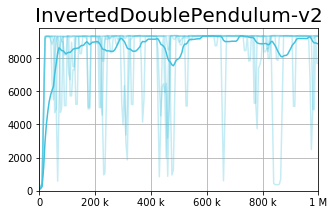
We observe that current policy gradient methods suffer from very high variance during the training process, as can be seen in the figures below (representing the TD3 [1] algorithm).
While the bold line represents the average performance across seeds, each light colored line represents a single seed. These results show that while TD3 is capable of finding relatively good policies, it suffers from very high instability - i.e., a policy which was good can become arbitrarily bad after a single gradient step.
We notice an interesting phenomena - the classic algorithms, Policy and Value Iteration, and the recent ones, DDPG and DQN, share similarities in the training procedure. For instance, when observing Policy Iteration side by side with the DDPG algorithm

these similarities become clear. Both algorithms go through a policy evaluation phase, in which the critic estimates the performance of the current policy, followed by a policy improvement phase in which the policy is improved with respect to the critic's estimation.
However, while these similarities exist, current policy gradient methods do not enjoy the expected behavior guaranteed in the classic approaches - stability and convergence.
How?
Off-policy methods usually employ a target policy network. The critic estimates the performance of the target policy, whereas the online policy is updated with respect to this estimation. As such, the online policy is expected to find the 1-step greedy update (a single Bellman update) with respect to the target policy.
However, the target policy is updated constantly using a Polyak Averaging technique. Our approach is simple and intuitive. We propose to update the target network periodically (as in the DQN [2]), yet only when the online policy has improved over the target (with high probability). The diagram below summarizes this approach.

The intuition for the success of such an approach is a simple random walk. When the random walk has a high probability of moving towards the right, the stationary distribution of the location of this process will be biased towards the right edge. As such, we expect that for a smaller value of 𝛿 the process will exhibit more stability.
* While a smaller value of 𝛿 increases stability, in practice, due to the variance in the MDP, it may be harder to find an improving policy - hence when 𝛿 is too small, the process may converge to a strictly sub-optimal solution.
Specifically, given K evaluations, we perform a t-test in order to predict whether or not the policy has improved with a high enough probability.
Experiments
On the right is the baseline (TD3), whereas on the left we present our approach, the Conservative TD3. We observe a slight improvement in the average result, yet a dramatic improvement in the per-seed variance reduction.

In this table, we calculate the variance (for each seed) across the last 100 evaluations during training. We present the worst (highest) variance observed across all 5 seeds. The results are clear - the conservative update rule reduces the variance dramatically, improving stability of the whole process.
Conclusions
We presented the Conservative Policy Gradient, an approach aimed to reduce the variance of the training process. Our approach is motivated by classical results and their similarity to the more recent deep-learning variants. While intuitive and simple, this approach is shown to work well.
Bibliography
[1] Fujimoto, Scott, Herke van Hoof, and David Meger. "Addressing function approximation error in actor-critic methods." arXiv preprint arXiv:1802.09477 (2018). [2] Mnih, Volodymyr, Koray Kavukcuoglu, David Silver, Andrei A. Rusu, Joel Veness, Marc G. Bellemare, Alex Graves et al. "Human-level control through deep reinforcement learning." Nature 518, no. 7540 (2015): 529.












Comments